Comparing currency trading strategies

In this example, we compare two strategies for trading currencies that differ only in the degree of the underlying model. We present an example in which the higher degree model outperforms the lower degree model.

We start by loading the necessary modules and functions.

%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import numpy as np
import pandas as pd
import os, fem, time
data_dir = '../../../data/currency'
cache = True
print 'number of processors: %i' % (fem.fortran_module.fortran_module.num_threads(),)

number of processors: 32

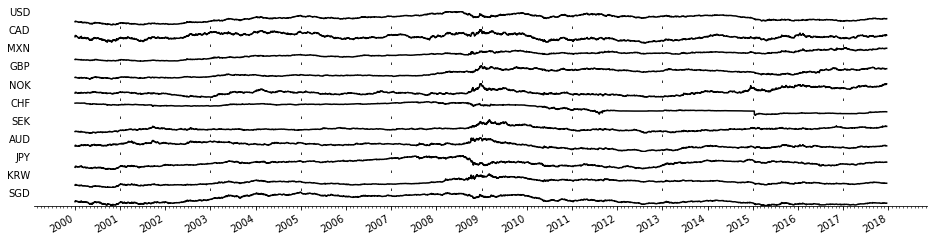
We use data of the currency exchange rates relative to the Euro from 2000 to 2018 for \(n=11\) currencies (USD, CAD, MXN, GBP, NOK, CHF, SEK, AUD, JPY, KRW, and SGD) plotted below.

# load data
currency = pd.read_csv(os.path.join(data_dir, 'currency.csv'), index_col=0)
x = currency.values.T

# plot data
fig, ax = plt.subplots(x.shape[0], 1, figsize=(16,4))
date2num = mdates.strpdate2num(fmt='%Y-%m-%d')
dates = [date2num(date) for date in currency.index]
for i, xi in enumerate(x):
    ax[i].plot_date(dates, xi, 'k-')
    ax[i].set_ylabel(currency.columns[i], rotation=0, ha='right')
    ax[i].set_yticks([])

for i in range(x.shape[0]-1):
    for spine in ['left', 'right', 'top', 'bottom']:
        ax[i].spines[spine].set_visible(False)
for spine in ['left', 'right', 'top']:
    ax[-1].spines[spine].set_visible(False)
ax[-1].xaxis.set_major_locator(mdates.YearLocator())
ax[-1].xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
ax[-1].xaxis.set_minor_locator(mdates.MonthLocator())
fig.autofmt_xdate()
plt.show()

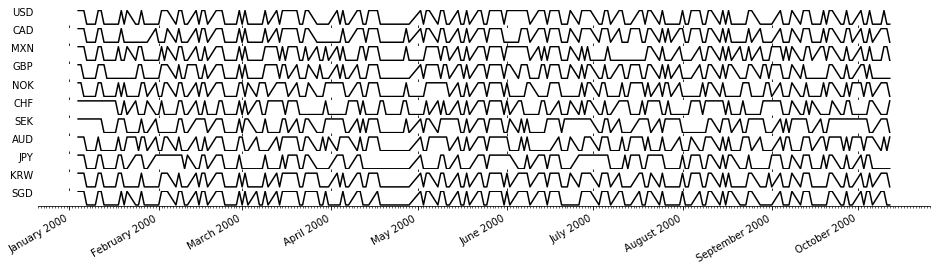
We discretize each currency exchange rate sequence \(\{x_i(t)\}_{t=t_1}^{t_{\ell}}\), where \(\Delta t=t_{k+1}-t_k=1\) day, by recording the sign of the daily movement \(\{s_i(t))\}_{t=t_2}^{t_{\ell}}\) with stagnation settled by the sign of the mean change:

\[\begin{split}s_i(t_{k+1}) = \begin{cases}1&\text{ if }x_i(t_{k+1})-x_i(t_k)>0\\-1&\text{ if }x_i(t_{k+1})-x_i(t_k)<0\\\text{sign}\left({1\over\ell-1}\sum_{k=1}^{\ell-1}(x_i(t_{k+1})-x_i(t_k))\right)&\text{ if }x_i(t_{k+1})-x_i(t_k)=0 \end{cases}.\end{split}\]

The first 200 fluctuations for each currency are plotted below.

# daily movement
dx = np.diff(x, axis=1)
# sign of daily movement
s = np.sign(dx).astype(int)
for i, si in enumerate(s):
    s[i][si==0] = np.sign(dx[i].mean())

fig, ax = plt.subplots(s.shape[0], 1, figsize=(16,4))

for i, si in enumerate(s):
    ax[i].plot_date(dates[1:201], si[:200], 'k-')
    ax[i].set_ylabel(currency.columns[i], rotation=0, ha='right')
    ax[i].set_yticks([])

for i in range(s.shape[0]-1):
    for spine in ['left', 'right', 'top', 'bottom']:
        ax[i].spines[spine].set_visible(False)
for spine in ['left', 'right', 'top']:
    ax[-1].spines[spine].set_visible(False)
ax[-1].xaxis.set_major_locator(mdates.MonthLocator())
ax[-1].xaxis.set_major_formatter(mdates.DateFormatter('%B %Y'))
ax[-1].xaxis.set_minor_locator(mdates.DayLocator())
fig.autofmt_xdate()
plt.show()

We fit two different models to the one-hot encodings of the binary data \(\{s_i(t)\}_{t=t_2}^{t_{\ell}}\). The one-hot encoding of \(s(t_k)=(s_1(t_k),\ldots,s_{n}(t_k))^T\in\{-1,1\}^n\) is a binary vector \(\sigma(t_k)=(\sigma_1(t_k),\ldots,\sigma_n(t_k))^T\in\{0,1\}^{2n}\) where \(\sigma_i(t_k)=(1,0)^T\) if \(s_i(t_k)=1\) and \(\sigma_i(t_k)=(0,1)^T\) if \(s_i(t_k)=-1\). In either model, the probability that \(x_i\) increases from \(t_k\) to \(t_{k+1}\) is assumed to be

\[p(s_i(t_{k+1})~|~s(t_k)) = {\exp e_{2i}^T h(\sigma(t_k))\over\sum_{i=1}^n\exp e_{2i}^Th(\sigma(t_k))}.\]

The two models differ in their definition of \(h\); in the first model, \(h(\sigma(t_k)) = W_1\sigma(t_k)\), but in the second model, \(h(\sigma(t_k)) = W_1\sigma(t_k) + W_2\sigma^2(t_k)\). The quadratic term \(\sigma^2\) consists of distinct nonzero products of the form \(\sigma_{j_2}\sigma_{j_1}\), \(1\leq j_1, j_2\leq 2n\) (see FEM for discrete data for more information on degrees of \(\sigma\)).

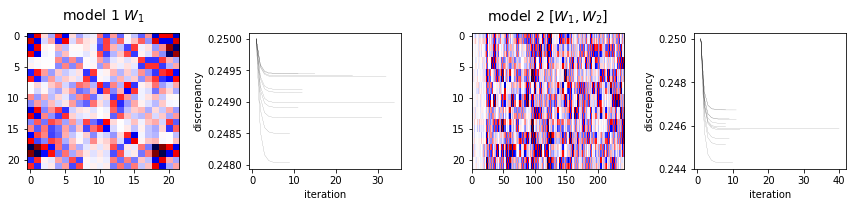
For demonstration, we instantiate two models, one with degs=[1] and one with degs=[1,2], and fit them to the whole currency data set. We plot the heat maps of the fitted model parameters and the running discrepancies during the fit for both models below.

# create two models
models = [fem.discrete.fit.model(degs=[1]), fem.discrete.fit.model(degs=[1, 2])]

# fit model to whole currency data set
for i, model in enumerate(models):
    start = time.time()
    model.fit(s[:,:-1], s[:, 1:], overfit=False)
    end = time.time()
    print 'model %i fit time: %.02f seconds' % (i+1, end-start)

# plot model parameter heat maps and running discrepancies
fig, ax = plt.subplots(1, 4, figsize=(12, 3))
for i, model in enumerate(models):
    w = np.hstack(model.w.itervalues())
    scale = np.abs(w).max()
    ax[2*i].matshow(w, cmap='seismic', vmin=-scale, vmax=scale, aspect='auto')
    ax[2*i].xaxis.set_ticks_position('bottom')
    for d in model.d:
        ax[2*i+1].plot(1 + np.arange(len(d)), d, 'k-', lw=0.1)
    ax[2*i+1].set_xlabel('iteration')
    ax[2*i+1].set_ylabel('discrepancy')
ax[0].set_title('model 1 $W_1$', fontsize=14)
ax[2].set_title('model 2 $[W_1, W_2]$', fontsize=14)
plt.tight_layout()
plt.show()

model 1 fit time: 0.13 seconds
model 2 fit time: 0.84 seconds

Next, we devise two simple trading strategies that train the models on a moving time window then predict \(s\) one day ahead of the window. We keep track of our account balances and prediction accuracies in the acccount and accuracy variables. The trading strategies work as follows. The models are trained on the data in the time window \([\) t1 \(,\) t1 \(+\) tw \(-1]\) to predict \(s(\) t1+tw \()\). Initially, t1 \(=\) t0, the initial time of the data set, and t1 is incremented by 1 while t1+tw is less than tn, the final time of the data set. On each day, we pass the data at t1 \(+\) tw to model.predict, which returns a prediction, 1 or -1, and probability greater than 0.5 of the price movement tomorrow. We select to trade only those currencies whose probabilities are greater than threshold, and we invest our whole account value weighted in the chosen currencies according the probabilities leveraged by a constant factor leverage. The models are retrained every dt days.

account_file = os.path.join(data_dir, 'account.npy')
accuracy_file = os.path.join(data_dir, 'accuracy.npy')

if cache and os.path.exists(account_file) and os.path.exists(accuracy_file):
    account = np.load(account_file)
    accuracy = np.load(accuracy_file)

else:
    # t0, tn: initial and final time
    t0, tn = 0, s.shape[1]

    # daily balance
    account = np.ones((2, tn))
    # daily prediction accuracy
    accuracy = np.zeros((2, tn))

    # tw: training time window width
    # dt: retraining period
    tw, dt = 200, 1
    # t1, t2: limits of moving training window
    t1, t2 = t0, t0+tw

    # maximum position weight
    max_weight = 1.0 / 3.0
    # trade if probability above threshold
    threshold = 0.75
    # percentage of account to bid
    leverage = 1.0

    start = time.time()
    while t2 < tn:

        # todays price
        price = x[:, t2]
        # tomorrows change
        realized_s = s[:, t2]
        realized_dx = dx[:, t2]
        percent_change = realized_dx / price

        for i, model in enumerate(models):

            # start todays account with yesterdays balance
            account[i, t2] = account[i, t2-1]

            # retrain the model
            if not (t1-t0) % dt:
                s_train = s[:,t1:t2]
                model.fit(s_train[:,:-1], s_train[:, 1:], overfit=False)

            # predict which currencies will increase
            prediction, probability = model.predict(s_train[:, -1])

            # trade if probability above threshold
            portfolio = probability > threshold
            if not portfolio.any():
                continue

            # position weights proportional to probability of prediction
            weights = (prediction * probability)[portfolio]
            weights /= np.abs(weights).sum()
            weights[weights > max_weight] = max_weight

            # take trading positions
            position = leverage * account[i,t2] * weights

            # calculuate returns and accuracy
            account[i, t2] += (position * percent_change[portfolio]).sum()
            accuracy[i, t2] = (prediction == realized_s)[portfolio].mean()

        t1 += 1
        t2 += 1

    end = time.time()
    print 'backtest time: %.02f minutes' % ((end-start)/60.,)
    np.save(account_file, account)
    np.save(accuracy_file, accuracy)

backtest time: 10.01 minutes

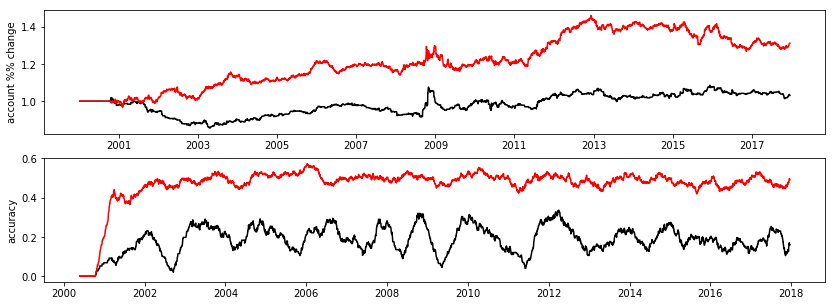
Finally, we examine which model performed better by plotting the account balance and rolling mean of the prediction accuracy. The model with the quadratic term performed better in by return and prediction accuracy.

accuracy_rolling_mean = pd.DataFrame(accuracy.T).rolling(100).mean().values.T
print 'accuracy: model 1: %.02f, model 2: %.02f' % (accuracy[0].mean(), accuracy[1].mean())

fig, ax = plt.subplots(2, 1, figsize=(14, 5))
ax[0].plot_date(dates[1:], account[0], 'k-', label='linear')
ax[0].plot_date(dates[1:], account[1], 'r-', label='quadratic')
ax[1].plot_date(dates[1:], accuracy_rolling_mean[0], 'k-')
ax[1].plot_date(dates[1:], accuracy_rolling_mean[1], 'r-')
ax[0].set_ylabel('account %% change')
ax[1].set_ylabel('accuracy')
plt.show()

accuracy: model 1: 0.18, model 2: 0.47